DVMP Simulation, Coverage, Trigger Rate and Background etc

Back to Main

Introduction

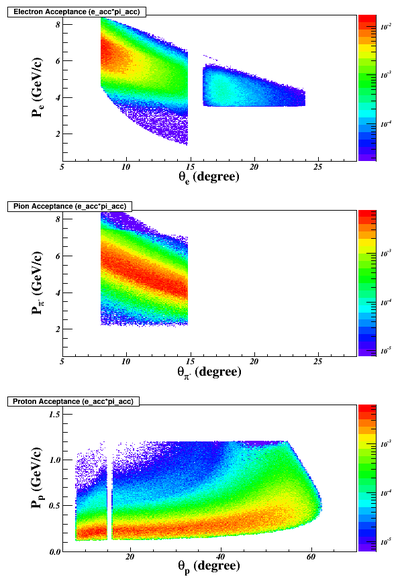
For all simulation and projection studies, we assume the DVMP run will be a parallel run with the SIDIS-He3 experiments with exact the same setup. On top of the SIDIS settings, we need to add a proton trigger to form a triple coincidence between electrons, pion- and protons. The existing SoLID detector after improving the timing resolutions, should be able to detect protons. We may can add a dedicate proton detector between the He3 target and the entrance of the CLEO-II magnet to cover a large range of the angle, from 24 degrees up to 65 degrees, with momentum ranges from 300MeV up to 1.2GeV. Simulation study shows that we can double the rates with this detector.

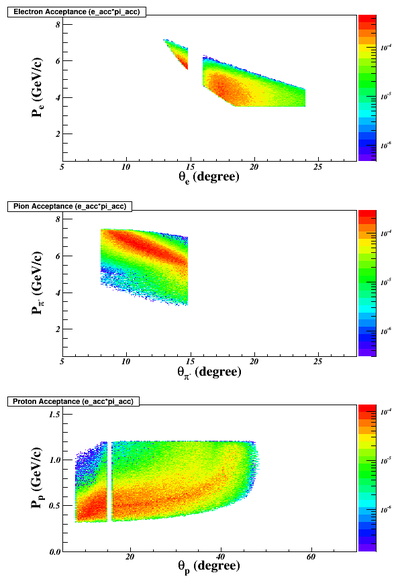
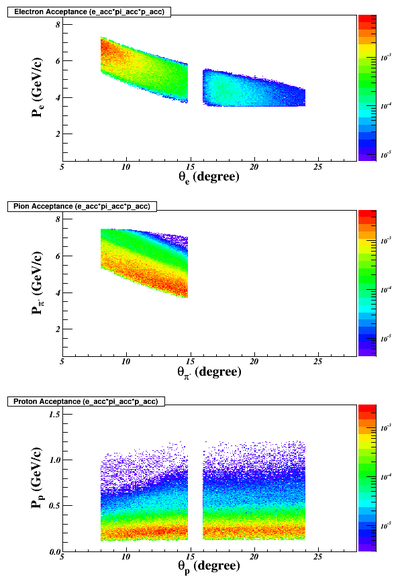
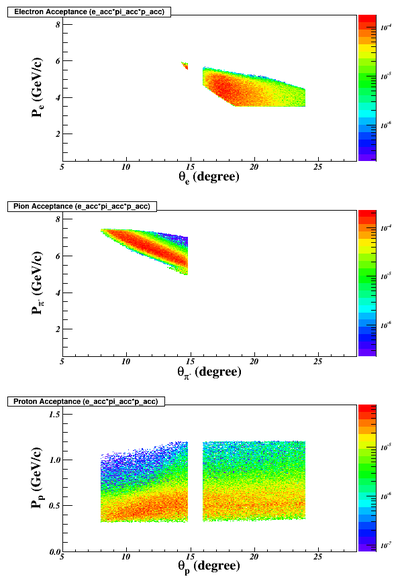
The phase space coverage of electrons and pions would be the same as one in the SIDIS experiment. The proton coverage depends on whether or not we use the recoil detector. On top of the kinematic requirements of SIDIS, the DVMP need to have Q2>4GeV^2 which can dramatically reduce the good event rates and make only the E0=11GeV beam energy setting useful. From now on, we will not consider the 8.8GeV setting.

The main background for the DVMP channel would be the SIDIS events which has 76KHz including physics rate and accidental coincidence rates. The background proton has 1.8MHz rate at forward+large angle regions. The triple coincidence with 30ns time window would reduce the accidental rate to 3.5KHz.

Coverage

• electron, pion and proton coverage w/ e+pi trigger (the current SIDIS trigger). They correspond to the case that we detect all protons by building a proton detectors. The second plot is w/ Q2>4 cut:

• electron, pion and proton coverage w/ e+pi+p trigger (the current SIDIS trigger + proton trigger using only existing SIDIS detectors). The second plot is w/ Q2>4 cut:

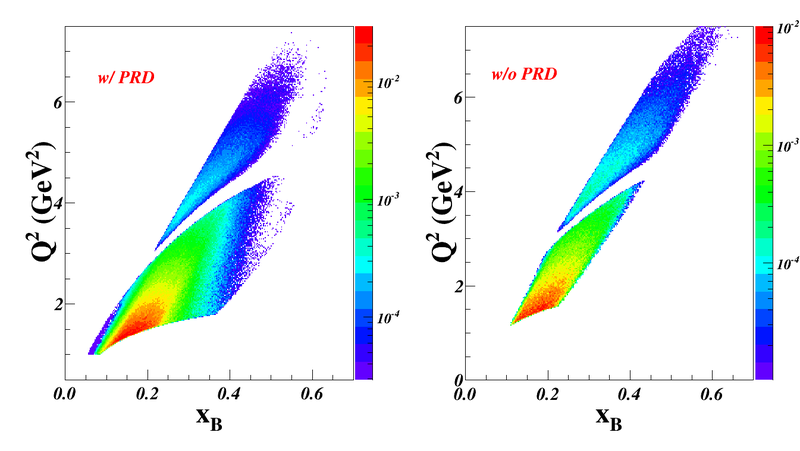
• Q2 vs. x. The left plot is the phase-space with protons detected by SoLID detectors and a recoil detector). The right plot is with proton detection by only the SoLID detectors (from 8 degrees ton 24 degrees)

Trigger Rate

The DVMP and SIDIS Physics Rates

Rates were estimated by weighting the randomly generated DVMP (SIDIS) events with the unpolarized cross sections, the total phase-space used to generate events, the target luminosity, and the acceptance of electrons and pions (and maybe protons if doing a triple coincidence measurement).

<math>R=PSF*Lumi*\sum_{k=1}^N_acc σ_k/N_gen * Acc_e * Acc_π </math>

Rate (Hz)	1<Q2<4 GeV2	Q2 >4 GeV2	Total
DVMP (e+pi+p)	17.79 (0.22)	0.53 (0.31)	26.45 (8.48)
SIDIS (e+pi)	1780.80	40.36	1821.16

Total Proton Rates from all backgrounds

The proton rates were simply counted right in front of the LASPD and FASPD w/o any trigger cuts (e.g. from LGC, HGC or EC). The hadron trigger is produced by MIP.

Rates in MHz	LA (all momentum ranges)	LA (w/ 0.2<$P_p$<1.2 GeV/c)	FA (all momentum ranges)	FA (w/ 0.2<$P_p$<1.2 GeV/c)
He3	3.511	1.38	6.93	1.39
He3 Up-Cell	2.66	0.97	1.92	0.57
He3 Down-Cell	2.58	1.08	2.17	0.68
Total	8.75	3.43	11.02	2.64

Projections

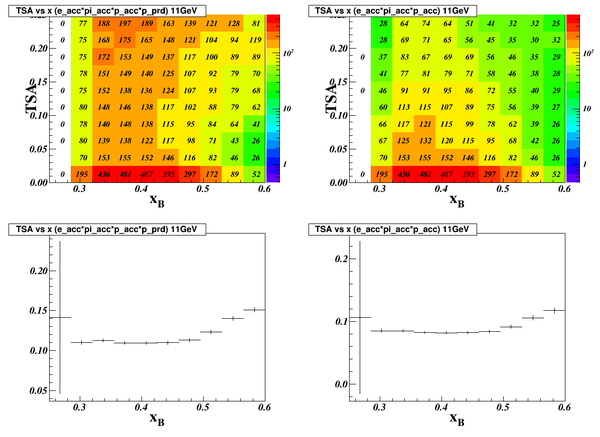
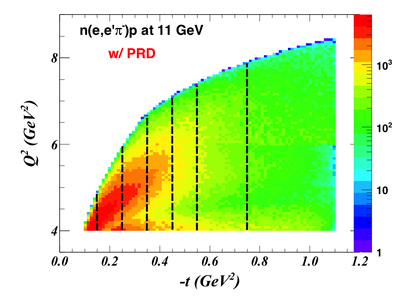
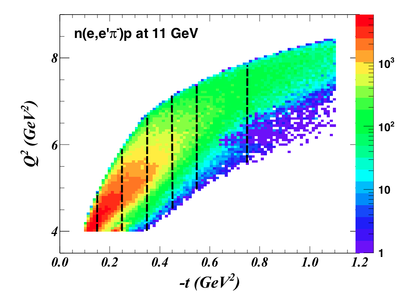
Here we are looking at how to bin the data. With such a low rate after Q2>4 cut (0.64Hz if detecting all protons, or 0.32Hz if just detecting protons with SoLID acceptance), we can not afford to bin on Q2 and Espilon. So we apply a cut, "Q2>4 && 0.55<Epsilon<0.75 && W>2.0", to integrate these variables, and only see if we can bin on t or x, or both.

At this time, I normalized the events rate by the target polarization (60%), effective neutron numbers (86.5%), and dilution factor of neutrons in He3 (90%). These terms go into the rate with a power of two. Then I applied the overall detector efficiencies (85%) and the beam time at 11 GeV (48 days). Hence, the rate you are going to see in the following plots should reflect the "projected real event counts" in each bin.

The following plots should the 1D binning of x or it and the average value of Target-Single-Spin Asymmetries in each bin. I simply binned in ten bins w/o optimize the bin-size. The plots sever as demonstration and we should discuss the final binning we want to present. Plots on the left are with detecting all proton using existing SoLID detector and a new recoil detector, while the plots on the right are w/o a new proton detector.

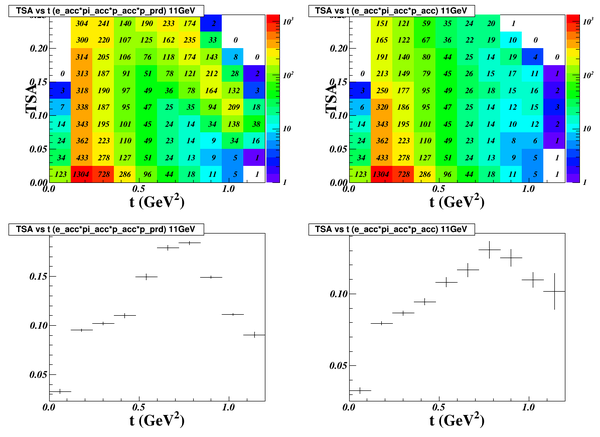
Here are more precious projected asymmetry results as a function of -t. 7 Bins were defined as shown in the next two plots, one is and one is w/o PRD.

Missing Mass and Background

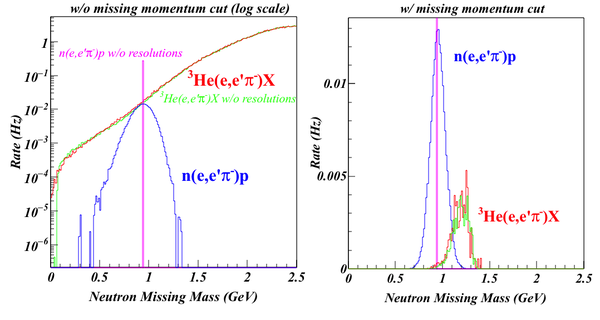
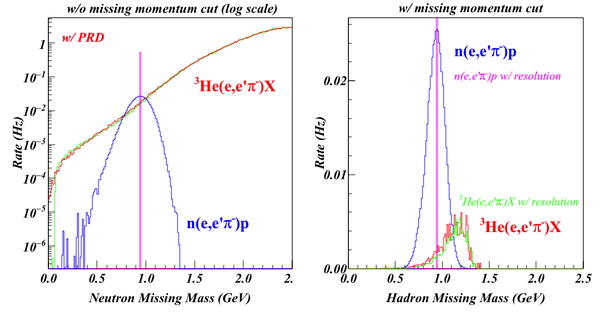
Our dominated background comes from the SIDIS reactions of electrons scattering on the neutron and two protons in He3. The neutron and proton SIDIS events were generated with the generator used for the SIDIS experiments. Both DVMP and SIDIS events were normalized to reflect the "actual" rates in Hz. No target polarization, dilution, inefficiencies and beam time are considered. When estimating the residual SIDIS results, I assumed the target fragments ("X") all contain one or more protons (simply since the SIDIS model don't know the branching ratio of producing protons in the target fragments), so we are overestimate the SIDIS rate. However, considering other proton channels (like proton-knock-out during QE) and accidental events, it may still be a good estimation, although I would expect the SIDIS peak would be much broader.

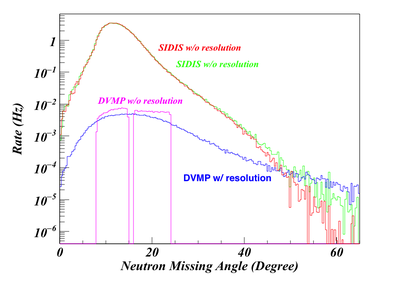
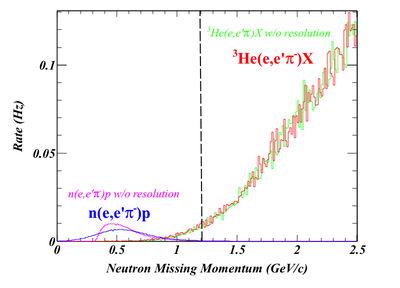
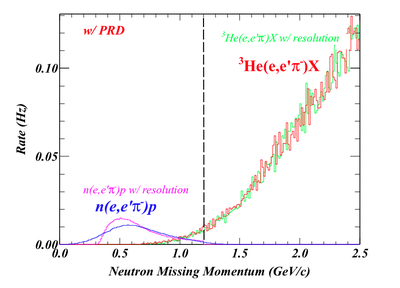
Besides, the missing mass, we also can reconstruct the missing momentum and missing angle of both the DVMP and SIDIS processes. As shown below, while the missing angles of DVMP and SIDIS events are overlapping largely, the missing momentum of two processes actually are well separated. If we apply a cut at P=1.2GeV, most of SIDIS background will be rejected. The case with the PRD is very similar.

With this idea, we exam the missing mass spectra of DVMP and SIDIS w/ and w/o the missing momentum cuts. w/o the cut, the SIDIS background overwhelms the DVMP peak (Of cause, the SIDIS rate is overestimated since I treat every "X" contains a proton). When applying the cut, the DVMP peak dominates and the SIDIS background is low. If we consider the fact that not every "X" in SIDIS contains a proton, the background will be much less. Although we haven't had a model to predict the ratio yet, we still can conclude that the SIDIS background won't be an issue.

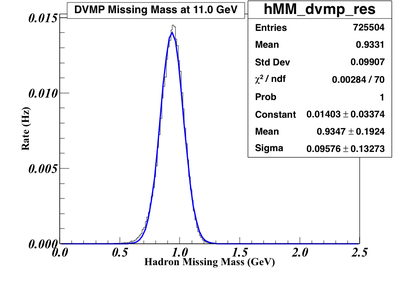
The next thing to do is to do a more sophisticated calculation of the missing mass. The figure below shows the current resolution of the missing mass spectra is about 100MeV when only taking into account the resolution effect from the SoLID detectors. We will need to consider the radiatve effect, the nucleon effect of the neutron inside He3, and also the Fermi-motion of the neutron in He3. The radiative effect can cause the asymmetry of the peak, while last two effects will further smear the peak. More background events can leak in because of that although the total background events are already small. I am working on estimating these effects.